A utilização da fórmula de Cardano
para solução de equações de 3º grau em problemas práticos logo
começou a apresentar resultados que desafiavam o entendimento
dos matemáticos da época. Seja por exemplo a equação x3
- 15x - 4 = 0 . Por simples verificação constata-se que x = 4
é uma de suas raízes ( as outras duas menos evidentes, são -2+Ö
` 3 e -2-Ö ` 3). Entretanto se tentarmos resolvê-la pela fórmula de
Cardano, teremos
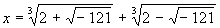
e caímos não apenas na extração de raízes quadradas de números
negativos, mas também na extração de raízes cúbicas de números
de natureza desconhecida. Esta é uma questão que não poderia ser
ignorada. Quando nas equações de 2º grau obtínhamos raízes de
números negativos, era fácil justificar que aquilo indicava a
inexistência de soluções. Agora, entretanto, estava-se diante
de equações com soluções evidentes, mas cuja determinação passava
pela extração de raízes quadradas de números negativos.
O que ocorria com a equação x3 - 15x - 4 = 0 pode
ser generalizado. Seja o polinomio
(x-a)(x-b)(x-c) = 0 cujas raízes são x = a, x = b e x = c . pesquisaremos
que relação deve haver entre a , b e c para que
o desenvolvimento conduza a uma equação do tipo x3
- px - q = 0 para a qual é valida a fórmula de Cardano
(x-a)(x-b)(x-c) = x3 - (a + b + c)
x2 +(ab + bc + ac)x - abc = 0
para que o termo de grau 2 se anule, é necessário que a
+ b + c = 0 ou seja c = -(a + b)
portanto , temos a equação (x - a) (x - b)(x + [a + b]) = 0.
Desenvolvendo :
x3 + [ab - (a + b)2] x +
ab (a + b) = 0
Aplicando-se a fórmula de Cardano tem-se
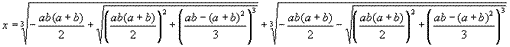
expressão que deve levar a x = a , x = b e x =
- (a + b) , soluções já conhecidas de antemão. Analisando
a expressão sob o radical quadrático ( chamaremos de D
, em analogia as equações de segundo grau )
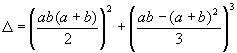desenvolvendo
temos
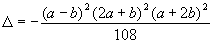mas se
a e b são reais , D nunca
será positivo
Esta é uma conclusão surpreendente pois, para que achemos a
e b distintos pela formula de Cardano, teremos obrigatoriamente
com raízes quadradas de números negativos. Não havia como negar
de que se estava diante de um tipo diferente de número. O homem
que consegui desvendar esse mistério foi Rafael Bombelli, nascido
em Bologna -Itália em 1536 e engenheiro hidráulico por profissão.
Conforme ele revelou em 1.572 no livro L'Algebra parte maggiore
dell' Arithmetica , seu método baseou-se no "pensamento
rude" segundo qual
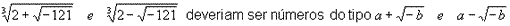assim
supondo, concluiu que a = 2 e b = 1, pois
ao realizar seus cálculos Bombelli criou as seguintes regras
para se operar com raiz de -1
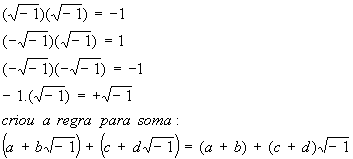
OBSERVAÇÃO : Foram as equações de 3º grau e não as de
2º que desencadearam todo desenvolvimento teórico dos números
complexos, trabalho que durou mais de 2 séculos a partir da idéia
de Rafael Bombelli
O Romance
das Equações Algébricas - G Garbi
