Em 1545 a forma
de resolução das equações cúbicas ( 3º grau) e das quádricas (4º
grau) tornam-se conhecidas com a publicação de Ars Magna de Girolamo
Cardano.
A publicação dessa obra causou tal impacto que 1545 é frequentemente
tomado como marco inicial do período moderno da matemática. Deve-se
frisar que Cardano (ou Cardan) não foi o descobridor original das
soluções quer das cúbicas, quer das quádricas.
Ele próprio admitiu isso em seu livro. A sugestão para resolver
as cúbicas, ele afirma, lhe tinham sido dadas por Niccolo Tartaglia.
A solução das quádricas tinha sido descoberta de seu antigo aluno,
Ludovico Ferrari.
O que Cardano deixou de mencionar em Ars Magna foi o solene juramento
que havia feito a Tartaglia de não revelar o seu segredo, pois este
pretendia firmar sua reputação publicando a solução das cúbicas,
até então desconhecida, em um tratado sobre álgebra.
Para que não se dê a Tartaglia a indevida simpatia, deve-se lembrar
que ele havia publicado, em 1543, uma tradução de Arquimedes, derivada
de Moerbeke, dando a impressão que a obra era sua.
E em seu Quesiti e invetioni diversi (Veneza-1546) ele deu a lei
do plano inclinado, presumivelmente derivada de Jordanus Nemorarius,
sem a devida atribuição.
Na verdade, é provavel que Tartaglia tenha recebido uma sugestão
quanto à resolução da cúbica de uma fonte mais antiga.
Qualquer que seja a verdade numa controvérsia um tanto complicada
e sórdida entre defensores de Cardano e Tartaglia, é claro que nenhum
dos dois foi o primeiro a fazer a descoberta.
O heroi no caso foi alguém cujo nome mal é lembrado hoje - Scipione
del Ferro ( cerca de 1465-1526) professor de matemática em Bologna,
uma das mais antigas universidades medievais e uma escola com forte
tradição matemática.
Como ou quando Ferro fez sua descoberta, não se sabe. Não publicou
a solução, mas antes de sua morte a revelou a um estudante, Antonio
Maria Fior.
Parece que a idéia da existência de solução algébrica para uma cúbica
se propalou, e Tartaglia nos conta que o conhecimento da possibilidade
de resolver a equação inspirou-o a dedicar-se a achar o método por
si.
Seja independente, seja baseado numa sugestão, Tartaglia de fato
aprendeu, por volta de 1541, a resolver equações cúbicas.
Quando a notícia disso se espalhou, foi organizada uma competição
matemática entre Tartaglia e Fior. Cada um dos concorrentes propos
trinta questões para que o outro resolve-se num intervalo de tempo
fixado.
Quando chegou o dia da decisão, Tartaglia havia resolvido todas
as questões propostas por Fior, enquanto este, não tinha resolvido
nenhuma das questões propostas pelo seu oponente.
A explicação é relativamente simples.
Hoje pensamos em equações cúbicas como sendo essencialmente todas
de um mesmo tipo e podendo ser todas resolvidas por um mesmo método.
Na época, porém, quando coeficientes negativos praticamente não
eram usados, havia tantos tipos de cúbicas quantas são as possibilidades
dos coeficientes positivos e negativos.
Fior só sabia resolver equações do tipo x3
+ px = q embora na época só fossem usados coeficientes numéricos
(positivos) específicos.
Mas enquanto isso, Tartaglia havia aprendido a resolver equações
do tipo em que cubos e quadrados são igualados a um número x3
+ px2 = q e sabia reduzir esse caso ao de
Fior.
A notícia do trunfo de Tartaglia chegou a Cardano, que logo convidou
o vencedor a visitar a sua casa, insinuando que trataria de arranjar
um encontro entre ele e um possível patrono.
Tartaglia não tinha nenhuma fonte substancial de recursos, em parte
talvez por um defeito na fala causada, na infância, por um golpe
de sabre sofrido durante a conquista da cidade natalde Breccia pelos
franceses em 1512.
Por esse fato, recebeu o apelido de tartaglia ( gago) , nome que
usou em lugar de Niccolo Fontana. Cardano , ao contrário lograra
sucesso como médico.
Tão grande era sua fama, que certa vez fora chamado a Escócia para
diagnosticar uma doença no Arcebispo de St Andrews.
De nascimento ilegítimo, e sendo astrólogo, jogador e herege, Cardano
foi no entanto um respeitavel professor em Bologna e Milão, e finalmente
recebeu do Papa uma pensão.
Cardano persuadiu Tartaglia a contar-lhe o segredo da solução das
cúbicas e fez um solene juramento de não divulga-lo, que evidentemene
foi quebrado com a publicação de Ars Magna.
Sobre a regra para resolver equações quádricas, Cardano escreveu
na Ars Magna que " é devida a Luigi Ferrari, que a inventou
a meu pedido ".
A resolução das equações cúbicas e quádricas foi talvez a maior
contribuição a álgebra desde que os babilônicos, quatro milênios
antes, apreenderam a completar o quadrado para equações quadráticas.
Nenhuma outra descoberta constitui um estímulo para o desenvolvimento
da álgebra comparável a essas reveladas em Ars Magna.
A resolução das cúbicas e quádricas não foi em nenhum sentido motivada
por considerações práticas, nem tinha valor para engenheiros.
Soluções aproximadas de algumas equações cúbicas ja eram conhecidas
na antiguidade, e al-Kashi, um século antes de Cardano, podia resolver
com qualquer grau de aproximação qualquer equação cúbica resultante
de problemas práticos.
A fórmula de Cardano-Tartaglia é de grande importância lógica, mas
nem de longe tão útil para as aplicações, quanto métodos de aproximações
sucessivas.
A History of Mathematics - Carl Boyer - John
Wiley & Sons, INC |
Esta curioso para
saber como se resolve a equação de 3º grau ?
Lembre-se
Tartaglia solucionara tipos especiais x3
+ px + q = 0 e x3
+ px2 + q = 0
e não a equação geral
ax3 + bx2
+ cx + d = 0 mas se fizermos x = y + m
e calculando m de modo a anular o termo de 2º grau, reduzimos a
equação completa em uma do tipo y3
+ py + q = 0
Seja ax3
+ bx2 + cx + d = 0
e x = y + m
a (y + m) 3
+ b (y + m) 2 + c (y
+ m) + d = 0
ay3
+ y2 (b + 3 am) + y
( 3 am2 + 2bm + c)
+( m3 a + bm2
+ cm + d) = 0
b + 3m = 0 Þ m =
- b / 3a
portanto se resolvermos a
equação y3
+ py + q = 0 acharemos x = y + m . A idéia
aqui é supor que a solução é a soma de duas parcelas Y =
A + B
Y 3
= ( A + B)3 Þ Y
3 = A3
+ B3 + 3AB ( A + B)
como Y = A + B temos Y 3
= A3 + B3
+ 3AB Y ou
Y
3 - 3AB Y- (A3+B3
) = 0 mas y3 + py +
q = 0 então p= -3AB e q = - (A3+B3
)
assim A3B3
= - p3/27 e
A3+B3
= - q
assim A3
e B3 são
números dos quais conhecemos a soma e o produto e este é um problema
classico de equação de 2º grau
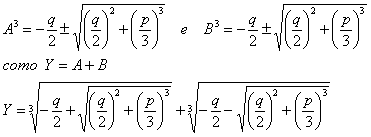
R
evista do Profesor de Matemática - nº 37 - Sociedade
Brasileira de Matemática |


