Eis
o racionio
A equação geral do 4º grau
ax4 + bx3
+ cx2 + dx + e = 0
sempre pode ser transformada em outra
do tipo
y4 + px2
+ qx + r = 0 fazendo x = y + m de modo
a anular o termo de 3º grau
Ferrari olhou para a equação x4
+ px2 + qx + r = 0
e procurou completa-la de modo a fatora-la num quadrado perfeito.
Se tal agrupamento fosse possível , seriam extraídas as raízes quadradas
e o problema recairia na solução de equações de 2º grau. Completando
a equação temos :
x4
+ (p + a)x2 + (r +
b) = ax2 - qx + b
para que os dois lados sejam
quadrados perfeitos, é preciso que os descriminantes sejam iguais
a zero simultaneamente

o que é uma equação do 3º
grau em a . Como as equações de 3º grau podiam ser resolvidas (
formula de Cardano) , acha-se a e em seguida b e extraiem-se
as raízes quadrada
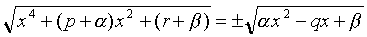
Para cada alternativa de
sinal + ou - tem-se uma equação do 2º grau, ambas com duas soluções.
PortAanto o método fornece 4 raízes .
| Passos para a solução geral de 4º |
1
- Toma-se a equação geral e faz-se a transformação do tipo
x = y + m de modo a transformar numa equação sem o termo de
3º |
2
- Reagrupam-se seus termos de modo a fazer com que ambos os
lados da igualdade sejam quadrados perfeitos. Cai-se numa
equação de 3º grau em a. Se ela for completa, faz-se
a transformação a = a ' + t de modo a obter-se uma equação
de 3º em a ' , sem o termo de 2º |
| 3
- Resolve-se a equação em a ' pelo método de Cardano |
| 4
- soma-se t a a ' e obtem-se a . Calcula-se b |
5
- Com a e b , extrai-se as raízes quadradas
dos dois lados da igualdade e obtem-se 4 valores possíveis
de y. Soma-se m a y e finalmente obtem-se as 4 raízes da equação
geral |
Realmente é um método perfeito, mas extremamete trabalhoso.
O grande mérito de Ferrari foi demosntrar que a solução das equações
de 4º grau eram possíveis somente com operações algébricas
Que tal tentar reolver a equação x4
+ 15 x2 - 10 x
+ 24 = 0
O Romance da Equações Algébricas - Gilberto G Garbi |


