O
conceito de infinito foi sempre uma pedra nos sapatos dos matemáticos
e ao longo da história provocou incontáveis discussões.
Já no século V a.C., o filósofo grego Zenão, apenas utilizando a
idéia de infinito, consegiu produzir paradoxos famosos, como o de
Aquiles não ser capaz de alcançar a tartaruga.
Na primeira metade do século XVII, o pai da física moderna, Galileu
Galilei, havia observado uma coisa que lhe parecera estranha.
Seja a sequência dos números naturais e ao lado de cada um deles
coloquemos seu quadrado:
| 1 |
|
|
|
1 |
| 2 |
|
|
|
4 |
| 3 |
|
|
|
9 |
| 4 |
|
|
|
16 |
| 5 |
|
|
|
25 |
| 6 |
|
|
|
36 |
| 7 |
|
|
|
49 |
| 8 |
|
|
|
64 |
| . |
|
|
|
. |
| n |
|
|
|
n2 |
Como para cada número da coluna da esquerda corresponde um e um
só número da coluna da direita e vice-versa, não temos dificuldades
em aceitar que as duas têm a mesma quantidade de elementos.
Entretanto, todos os números da direita também podem ser encontrados
à esquerda, ou seja, como observou Galileu, no conjunto infinito
dos naturais a parte era igual ao todo.
Ocorre que para qunatidades finitas o axioma de que a parte é sempre
menor que o todo era uma verdade indiscutível há séculos.
O teorema segundo o qual, em um triângulo, qualquerângulo externo
é maior do que os internos não adjacentes foi demosntrado por Euclides nos elementos precisamente com base na idéia de que a
parte é sempre menor que o todo.
No mundo das infinitudes, este axioma deixará de ser válido, em
mais um exemplo dos riscos que se corre ao generalizar para o infinito
conceitos que são verdadeiros para entidades finitas.
Cantor começou procurando atribuir "tamanhos", que ele
chamou de potências, aos diversos tipos de conjuntos de infiniitos
elementos.
Ao conjunto dos números inteiros 1,2,3,...(aquele que Kronecker
disse ter sido o único criado por Deus) foi atribuída a potência
representada pela primeira letra do alfabeto hebraico À0 (lê-se Alef-zero),
que é o menor dos números transfinitos .
Este transfinito À0 (Alef-zero), potência do conjunto
dos números naturais, foi uma espécie de unidade de medida que Cantor
passou a utilizar para estudar outros conjuntosde infinitos elementos.
Quando os elementos de um conjunto podem ser colocados em correspondência
biounívoca com o conjunto dos números naturais, diz-se que ele é
contável ou enumerável e que sua potência também é À0 (Alef-zero).
Cantor provou que existem infinitas potências diferentes de conjuntos
infinitos.
O primeiro conjunto a ser comparado com os dos números naturais
foi o dos racionais. Cantor dispôs aqueles números em sucessivas
linhas horizontais, cada um denominador a partir de 1.
Os numeradores, em cada linha crescem da esquerda para a direita.
É fácil ver que todos os números racionais positivos estão contidos
no quadro, inclusive as repetições com 1/2 , 2/4, 3/6, etc ( para
os negativos vale o mesmo raciocínio)
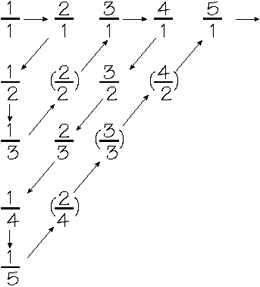 |
Seguindo
o esquema de flechas na figura, vê-se que podemos contar os racionais,
inclusive desconsiderando as repetições que aparecem entre parenteses.
Portanto a potência dos racionais é a mesma dos naturais, ou seja,
À0 (Alef-zero).
O passo seguinte foi estudar os algébricos e Cantor descobriu através
de um raciocínio mais elaborado que esles também são contaveis e
assim sua potência também é À0 (Alef-zero).
Continuando, por um método simples e elegante, Cantor provou que
os números reais não são contaveis e chamou a potência daquele conjunto
de C (de contínuo) ou À1 (Alef-um).
Para prová-lo, Cantor supôs o oposto, ou seja, que os reais são
contaveis. Assim sendo, a partir do zero, eles deveriam poder ser
colocados em uma sequência da forma :
1 ® 0, a11
a12 a13 ....
2 ® 0, a21 a22 a23 ..
3 ® 0, a31 a32 a33 ..
|
e assim por diante, indefinidamente,
onde os diversos a's são dígitos de 0 a 9.
Ora qualquer número do tipo 0,b1b2b3b4
..... onde b1¹a11 ,b2¹a22,
b3¹a33....... diferirá dos 0,aij
por pelo menos um dígito, ou seja, estará fora da lista que deveria
conter todos os reais, se eles fossem contáveis. Portanto não são.
Esta prova, alias, é uma demosntração indireta de que existem os
trancendentes, pois se os reais não são contáveis e se os algébricos
o são, então existem reais não algébricos (e não contáveis), ou
seja, transcendentes.
Desta forma ficou demosntrado que existem muito mais números transcendentes
do que algébricos.
Os trabalhos de Cantor sobre os transfinitos bastante masi além.
Ele demonstrou proposições que desafiam nosso entendimento, habituado
a um mundo de coisas finitas, como, por exemplo, que em qualquer
intervalo real (a,b) por menor que seja, existem tantos números
quanto em todo conjunto dos reais ( novamente a parte é igual ao
todo) Teoremas ainda masi espantosos podem ser encontrados entre
suas descobertas.
Cantor foi muito amigo de outro famoso matemático de fim do século
XIX, Richard Dedekind, o homem que deu sólido fundamento lógico
a teoria dos números reais.
Ambos costumavam discutir entre si suas idéias sobre números reais
e transfinitos de modo que na matemática os nomes de Cantor e Dedekind
quase sempre aparecem associados.
Cantor faleceu em 1918, tristemente internado em um hospital para
enfermos mentais, mas é pouco provável que a causa da doença tenha
sido seu esforço em pensar o impensável.
|


